
Busca linear (sequencial) Link para o cabeçalho
A busca linear é uma forma de pesquisar em um conjunto de dados de maneira sequencial, elemento por elemento. Ela recebe esse nome porque o seu tempo de execução cresce proporcionalmente a quantidade de elementos que existem no conjunto - ou seja, tem um crescimento linear.
O funcionamento é muito simples: dado um conjunto de dados, verificamos os elementos um a um, do início ao fim, até encontrarmos o valor desejado ou chegarmos ao final da lista.
Exemplo Link para o cabeçalho
Imagine que você tem um caderno de anotações, onde escreve diversas ideias, frases soltas, nomes ou tarefas ao longo do dia. Em um certo momento, você se lembra que anotou nele a lista de compras do mercado, mas não faz ideia de em qual página ela está. O que lhe resta fazer? Folhear as páginas do caderno uma a uma, do começo ao fim, até encontrar onde a lista está anotada. É exatamente assim que a busca linear funciona. Vejamos esse cenário em Go.
Código fonte Link para o cabeçalho
package main
import (
"fmt"
"strings"
)
func buscaPalavra(caderno []string, palavra string) int {
for i, pagina := range caderno {
if strings.Contains(pagina, palavra) {
return i
}
}
return -1
}
func main() {
caderno := []string {
"Ligar para o João",
"Estudar algoritmos à noite",
"Marcar reunião com a equipe",
"Lista de compras: pão, leite e ovo",
"Ver filme no sábado",
}
palavra := "compras"
pagina := buscaPalavra(caderno, palavra)
if pagina != -1 {
fmt.Printf("A palavra '%s' foi encontrada na página %d: \"%s\"\n", palavra, pagina + 1, caderno[pagina])
} else {
fmt.Printf("A palavra '%s' não foi encontrada no caderno.\n", palavra)
}
}
Repare que nosso “caderno” é representado por um slice de strings, onde cada string é uma página. Nesse caso estamos folheando o caderno atrás da palavra “compras” e é isso que passamos para a função buscaPalavra.
Dentro da função, nós percorremos página por página utilizando string.Contains, que verifica se aquela página possui a palavra que estamos procurando. Por sorte, nosso caderno não é muito grande e encontramos a nossa lista de compras na página 4, produzindo o seguinte resultado:
A palavra 'leite' foi encontrada na página 4: "Lista de compras: pão, leite e ovo"
Mas o que aconteceria se procurássemos pela palavra “mercado”? Repare que nesse caso essa palavra não está escrita em nenhuma das páginas e portanto nós chegaríamos ao final do caderno sem encontrar o que procuramos.
Quando isso acontece, é comum retornar um valor especial que indique a ausência do elemento. Uma convenção comum é retornar -1, já que essa não é uma posição válida dentro do nosso conjunto de dados.
Análise de complexidade Link para o cabeçalho
A complexidade do algoritmo de busca linear é O(n), o que significa que seu tempo de execução é proporcional ao tamanho do conjunto. Por esse motivo, ela não é eficiente para grandes volumes de dados.
Voltando ao nosso exemplo: se o caderno tivesse 500 páginas ao invés de 5, o número de verificações aumentaria significativamente — e com ele, o tempo de execução da busca.
Busca binária Link para o cabeçalho
A busca binária é uma forma mais eficiente de pesquisar em um conjunto de dados. O algoritmo funciona dividindo repetidamente um conjunto ao meio e comparando o valor mediano com o valor procurado. O resultado da comparação determina se o algoritmo repete o processo com o subconjunto da esquerda ou da direita, até que sobre apenas uma possível localização para o elemento.
Apesar de ser extremamente eficiente, há um porém: o conjunto de dados deve estar ordenado para que o algoritmo funcione. Vamos a um exemplo ilustrativo para que a ideia do algoritmo fique mais clara.
Considere o seguinte conjunto de elementos. Nesse conjunto queremos encontrar o elemento 34.

A primeira coisa que devemos fazer é determinar o início e o fim dentro do nosso conjunto, ou seja, de qual até qual posição iremos procurar o nosso elemento. Como estamos começando a busca e ainda não temos nenhuma pista de onde o 34 está, nosso início será em P0 e o fim em P7. Após definirmos o início e fim, devemos definir a posição que representará o meio do nosso conjunto. O meio é calculado por (Fim+início)/2. No nosso caso (7+0)/2 = 3,5. Como 3,5 não é uma posição válida, iremos considerar sempre apenas a parte inteira do resultado, nesse caso P3. Dessa forma, comparamos: o elemento em P3 (20) é igual ao elemento buscado (34)?

A resposta é não. Então devemos seguir para a próxima etapa do algoritmo: reduzir o espaço de busca. Para isso verificamos o seguinte: o elemento em P3 (20) é menor que o alvo (34)? A resposta é sim. E o que isso significa? Significa que como P3 não possui o elemento que estamos buscando e o elemento dele é menor do que o buscado, então podemos afirmar que todos os elementos das posições anteriores a P3 podem ser descartados, uma vez que eles possuirão elementos com valor no máximo igual ao de P3. Portanto, é correto atualizar nossa posição de início e dizer que nosso espaço de busca agora será de P4 (meio +1) até P7.

Agora repetimos o processo e calculamos um novo meio: (7+4)/2 = 5. E então verificamos: o elemento de P5 (59) é igual ao buscado (34)?
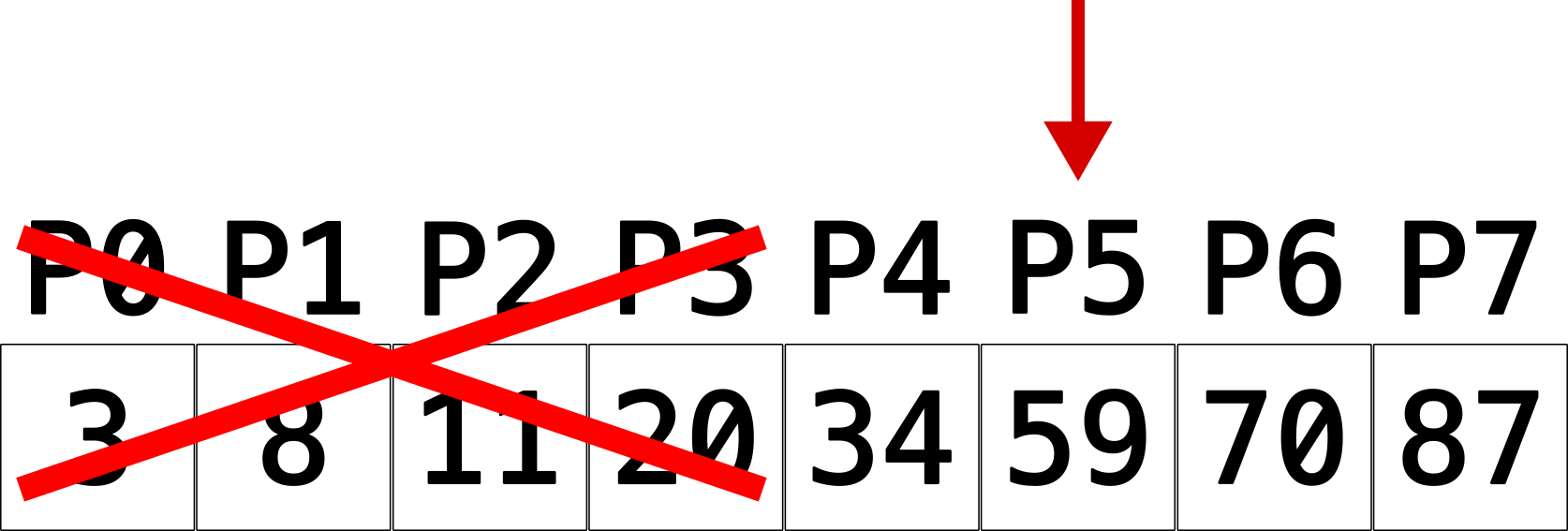
A resposta é não. Seguimos novamente para a próxima etapa: redução do espaço de busca. Verificamos então: o elemento em P5 (59) é menor que o alvo (34)? A resposta é não novamente. Então sabemos que o elemento busca não está nas posições P5 em diante. Vamos então manter a nossa posição de início de busca e reduzir a posição de fim. Nossa posição de fim sai de P7 para P4 (meio - 1).

Repetimos mais uma vez o processo e calculamos o meio (4+4)/2 = 4. Então verificamos: o elemento de P4 (34) é igual ao buscado (34)?
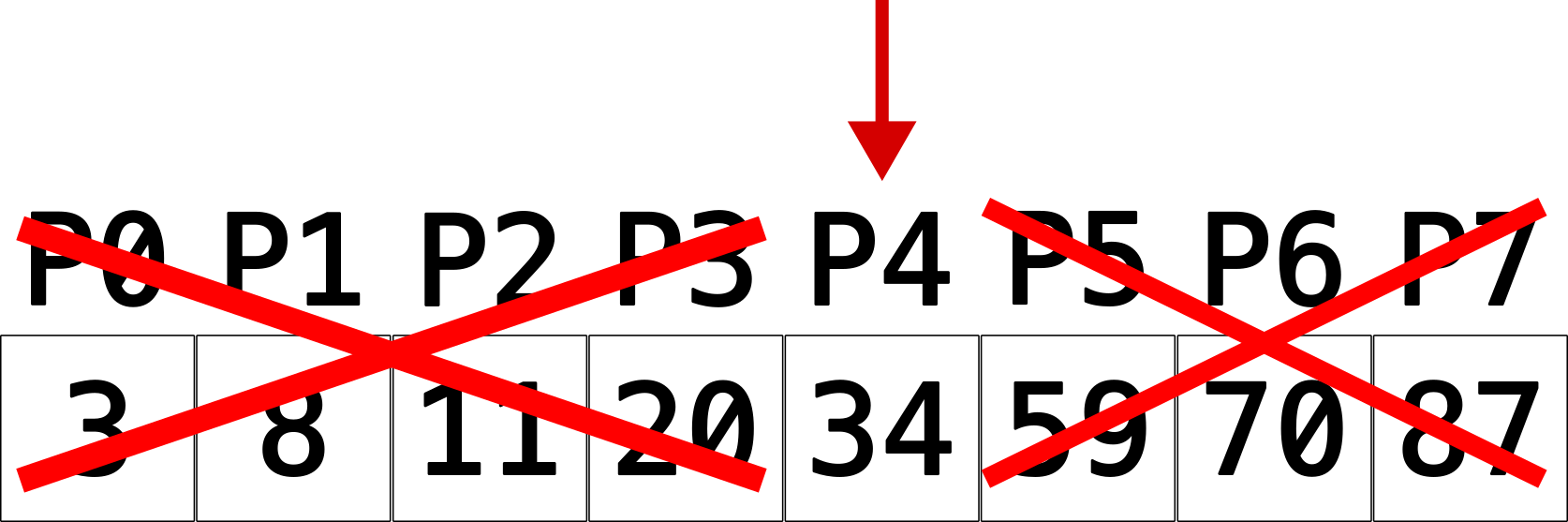
Sim! Com isso concluímos nossa busca e podemos dizer que o elemento foi encontrado na posição P4.
Código fonte Link para o cabeçalho
package main
import (
"fmt"
)
func buscaBinaria(arr []int, alvo int) int {
inicio := 0
fim := len(arr) - 1
for inicio <= fim {
meio := (inicio + fim)/2
if arr[meio] == alvo {
return meio
} else if arr[meio] < alvo {
inicio = meio + 1
} else {
fim = meio - 1
}
}
return -1
}
func main() {
dados := []int {3, 8, 11, 20, 34, 59, 70, 87}
alvo := 34
posicao := buscaBinaria(dados, alvo)
if posicao != -1 {
fmt.Printf("Elemento %d encontrado na posição %d\n", alvo, posicao)
} else {
fmt.Printf("Elemento %d não encontrado\n", alvo)
}
}
Análise de complexidade Link para o cabeçalho
A busca binária é um algoritmo eficiente para encontrar elementos em conjuntos ordenados. Sua principal vantagem é reduzir pela metade o espaço de busca a cada iteração. A complexidade do algoritmo de busca binária é O(log n), o que significa que seu tempo de execução cresce de forma logarítmica, o que a torna muito eficiente para grandes conjuntos de dados.
Comparativo Link para o cabeçalho
| Característica | Busca linear | Busca binária |
|---|---|---|
| Estrutura precisa ser ordenada? | ❌ Não | ✅ Sim |
| Velocidade (grandes listas) | 🐢 Lenta (O(n)) | ⚡ Rápida (O(log n)) |
| Implementação | ✅ Simples | 🔁 Exige ordenação |
| Ideal para | Poucos dados | Muitos dados |